교재 기준 p.50
# 문제 005 나머지 합 구하기


문제 링크
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
연속된 부분의 합을 다 고려하고 문제를 풀어야 된다...
이때 문제의 제한 시간이 있다.
구간 합 배열을 이용해야 되는 문제라는 것을 알 수 있다.
먼저 내가 처음으로 생각했던 문제 풀이 과정은
(1). 먼저 첫 번째 줄에 N, M을 입력받는다. (N개의 수를 입력받을 건지, 합이 임의의 수 M으로 떨어지게 할 건지 정의)
(2). 두 번째 줄에 N개의 수를 입력받는다.
(3). N의 수의 구간 합 배열을 구한다.
(4). 구간 합 배열을 M으로 나눈다.
(5). %이 0인 숫자만 남긴 뒤에 개수를 센다.
이었다 그러나, (5)까지의 과정은 처음부터 해당 수까지 모두 더했을 때 %0인 숫자만 고려한 것이다... 무슨 말인지 이해가 안 될것이다.
설명을 해보자면
1 0 3 3 4
란 숫자가 들어왔다 생각해보자
이때 합 배열을 구하게 되면
1 0 4 7 11이 된다.
이때 M이 3이라고 하면
%3을 했을 때 0이 되는 숫자는 없다. 그러나 1 0 3 3 4 중에 연속된 값인 3 3을 더해준 값 6을 %3 하면 0이 된다.
이렇게 (5)까지의 과정은 해당 순서까지의 값을 모두 더한 값만 고려한 것이므로 또 다른 과정이 필요하다.
즉, 해당 순서까지의 값을 모두 더한 값 뿐만 아니라 중간에서 시작해서 연속된 값들도 고려해줘야 된다.
=> S[i]만 고려해주는 것이 아니라 S[j] - S[i]도 고려해줬어야 됐다... (이때 당연히 i는 j보다 작아야 됨. 그래야 중간 부분의 합이 될 것)
이 문제에서는 모듈로 연산의 기본 개념을 알고 있으면 쉽게 풀리는 문제다.
https://mikrkosmos97.tistory.com/130
모듈로 연산 (Modulo Operation)
모듈로 연산 어떤 한 숫자를 다른 숫자로 나눈 나머지를 구하는 연산으로, 나머지 연산(mod)이라고 한다. 정수론에서 모듈라 연산(modular arithmetic)이란, 정수의 합과 곱을 어떤 주어진 수의 나머지
mikrkosmos97.tistory.com
모듈로 연산에 대하여 정리한 게시글이다. 참고하는 것도 좋을 듯! (ㅎㅎ)
모듈로 연산의 속성에 대하여 다시 한번 고려해보자.

우리는 현재 부분 합은 S[j] - S[i]에 mod n을 했을 때 0인 숫자를 구하려 하고 있다.
그러면 두 번째 공식을 통해 문제를 해결할 수 있을 것이다.
S[j]를 a S[i]를 b라 생각해보자
우리가 현재 구하는 것은 (a - b) mod n이 0인 값이다.
이를 두 번째 공식에 대입해보면
0 = ((a mod n) - (b mod n)) mod n이 되고
결국 (a mod n)과 (b mod n)이 같다면... mod n은 0 이 될 것이다.
즉 우리는 mod n을 했을 때 같은 값이 나오는 두 쌍을 가져와서 경우의 수를 구해주면 될 것이다.
(이 결론을 이끌어내기까지 어려웠다...)
이제 문제를 풀어보자
먼저 첫번째 줄에 정수 N, M을 입력받고, 두번째 줄에 N개의 수를 입력받아야 된다.
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
nList = list(map(int, input().split()))
이때 합 배열을 생성해준다. 이때 n개의 개수의 합이 생기므로 입력받은 n개를 이용여 합배열을 만들어준다.
이때 S[0]에 대한 정의가 필요한데 S[0]은 nList[0]의 값이 된다. (첫 번째 인자만 더한 값이 S[0]이므로)
그리고 정답을 받아줄 변수를 0으로 초기화한다.
S = [0]*n
S[0] = nList[0]
result = 0
이제 합 배열을 저장해줄 차례다.
for i in range(1, n):
S[i] = S[i-1] + nList[i]
S[0]은 이미 정의된 상태이므로 S[1]부터 S[n]까지 구해주면 된다.
합 배열을 저장했으니 이제 합 배열을 M으로 나눈 나머지 값이 0인 수들을 구해준다.
이때 해당 조건에 맞는 숫자면 result 값을 증가시킨다. (여기까지 위의 풀이에 (5) 구간)
C = [0]*m
for i in range(n):
rm = S[i] % m;
if rm == 0:
result += 1
C[rm] += 1
위의 코드를 보면 S[i]를 m으로 나눈 나머지값을 rm이란 변수에 넣어주고 0일 때 result 변수를 증가시켰다.
이때 C[rm]에 1을 증가시킨다. C[rm]은 뭘까?
위에서 합 배열에서 나머지가 0이 되는 숫자뿐만이 아니라
나머지가 같은 숫자쌍도 경우의 수가 될 수 있다고 언급했다...
그리고 C는 같은 나머지의 숫자를 카운트해줄 리스트다.
여기서 rm의 경우의 수는 0~m-1이다.(m으로 나눈 나머지기 때문에 m보다 클 수 없음)
따라서 C의 최대 크기는 m개일 것이다.
C[rm] +=1 을 해주면 나머지가 같은 인덱스가 자동으로 조건에 맞게 증가할 거고 여기까지가 위의 코드다.
우리는 for문을 m번 돌리면서 rm이 1 이상인 인덱스만 뽑아내서
쌍이 되는 경우의 수만 result에 더해주면 되는 것이다. 즉 같은 원소 값이 같은 2개의 원소를 뽑는 모든 경우의 수를 구해야 된다.
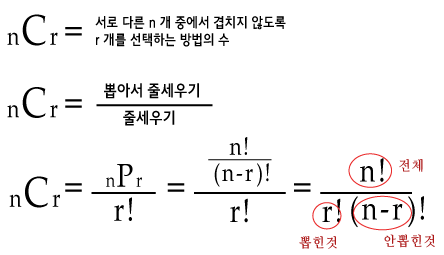
nC2...를 구해야 된다는 것인데 nC2는 n(n-1)/2와 같다.
이 과정은 아래에 짜보자.
for i in range(m):
if C[rm] > 1:
result += (C[i]*(C[i]-1) // 2)/ 대신 //를 사용한 이유는 int의 결과를 얻어내기 위해서다.
이런 방법으로 result의 값을 구할 수 있다.
만약 합이 M으로 나누어 떨어지는 (i, j) 쌍을 모두 구하라고 했으면 이렇게 풀 수 없을 것이다.
하지만 우리는 쌍의 개수만 구하면 되므로 경우의 수만 정확하게 구해내면 되기에 이런 방법을 사용하여 풀 수 있었다.
따라서 전체 코드는
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
nList = list(map(int, input().split()))
S = [0]*n
C = [0]*m
result = 0
S[0]=nList[0]
for i in range(1, n):
S[i] = S[i-1] + nList[i]
for i in range(n):
rm = S[i] % m;
if rm == 0:
result += 1
C[rm] += 1
for i in range(m):
if C[rm] > 1:
result += (C[i]*(C[i]-1) // 2)
print(result)
굿!
'코딩 테스트 준비' 카테고리의 다른 글
| 모듈로 연산 (Modulo Operation) (0) | 2022.12.13 |
|---|---|
| [Python] 백준 11659 문제 풀이, 구간 합, 입출력 속도 개선 (0) | 2022.12.05 |
| [Python] 백준 11720, 1546 문제 풀이, 배열과 리스트 (1) | 2022.12.02 |
| [Python] 백준 2798 문제 풀이, 브루트 포스 (1) | 2022.12.01 |
| [Python] 프로그래머스 옹알이(1) 문제 풀이 (0) | 2022.11.30 |

